容器,就是用来存放东西的盒子。
常用的容器包括:数组array, 链表list, 树tree, 栈stack, 队列queue, 散列表hash table, 集合set、映射表map 等等。容器便是容纳这些数据结构的。这些数据结构分为序列式与关联式两种,容器也分为序列式容器和关联式容器。
STL 标准模板库,核心包括容器、算法、迭代器。
元素排列次序与元素无关,由元素添加到容器的顺序决定
一、序列式容器/顺序容器
| 容器 | 说明 |
|---|---|
| vector | 支持快速随机访问 |
| list | 支持快速插入、删除 |
| deque | 双端队列 允许两端都可以进行入队和出队操作的队列 |
| stack | 后进先出LIFO(Last In First Out)堆栈 |
| queue | 先进先出FIFO(First Input First Output)队列 |
| priority_queue | 有优先级管理的queue |
1. 向量(vector)
连续存储的元素
迭代器的实现
1 | //获得指向首元素的迭代器 模板类,不是指针,当做指针来使用 |
2. 列表 (list)
由节点组成的双向链表,每个结点包含着一个元素
3. 双端队列(deque)
连续存储的指向不同元素的指针所组成的数组
4. 栈(stack)
后进先出的值的排列
1 | stack<int> s; |
5. 队列(queue)
先进先出的值的排列
1 | queue<int> q; |
6. 优先队列(priority_queue )
元素的次序是由所存储的数据的某个值排列的一种队列
1 | //最大的在队首 |
二、关联式容器
关联容器和大部分顺序容器操作一致
关联容器中的元素是按关键字来保存和访问的 支持高效的关键字查找与访问
1. 集合(set)
由节点组成的红黑树,每个节点都包含着一个元素,元素不可重复
1 | set<string> a; |
2. 键值对(map)
由{键,值}对组成的集合
1 | map<int, string> m; |
unordered_map
c++11取代hash_map(哈希表实现,无序)
哈希表实现查找速度会比RB树实现快,但rb整体更节省内存
需要无序容器,高频快速查找删除,数据量较大用unordered_map;
需要有序容器,查找删除频率稳定,在意内存时用map。
3. 红黑树
红黑树(Red Black Tree)又称为 RB树,是一种相对平衡二叉树 。
1.节点是红色或黑色。
2.根节点是黑色。
3.每个叶子节点(空节点)都是黑色的。
4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
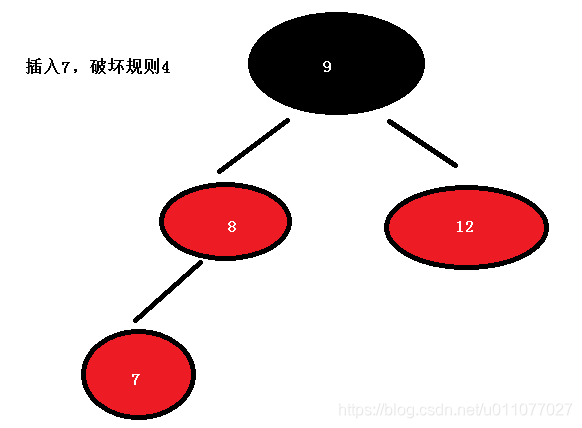
- 插入新节点总是红色节点
- 如果插入节点的父节点是黑色, 能维持性质
- 如果插入节点的父节点是红色, 破坏了性质。插入算法就是通过重新着色或旋转, 来维持性质
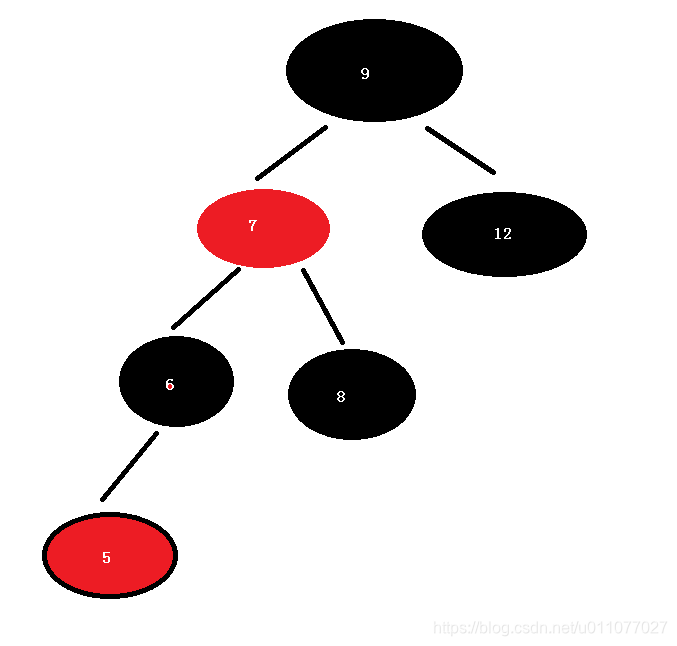
插入 7 后,破坏了规则,那么需要根据不同的状况进行不同的策略使其平衡并符合规则。
7的父节点8 与叔父节点 12 都是红色,则我们可以将8、12两个重绘为黑色并重绘祖父节点9为红色。
这里9是根节点,为了满足规则1,又把它重绘为黑色 .
经过调整:
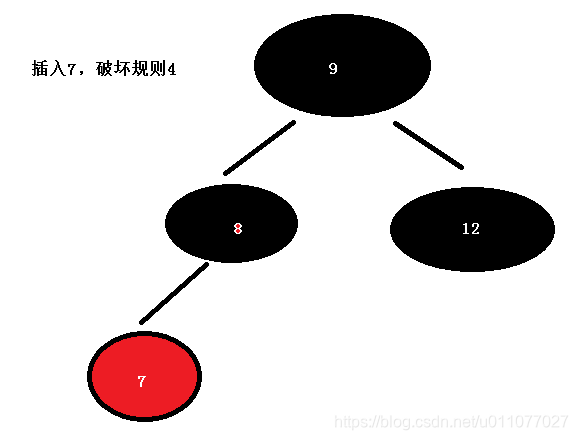
现在满足5个规则,因此7插入完成。
接下来插入 6
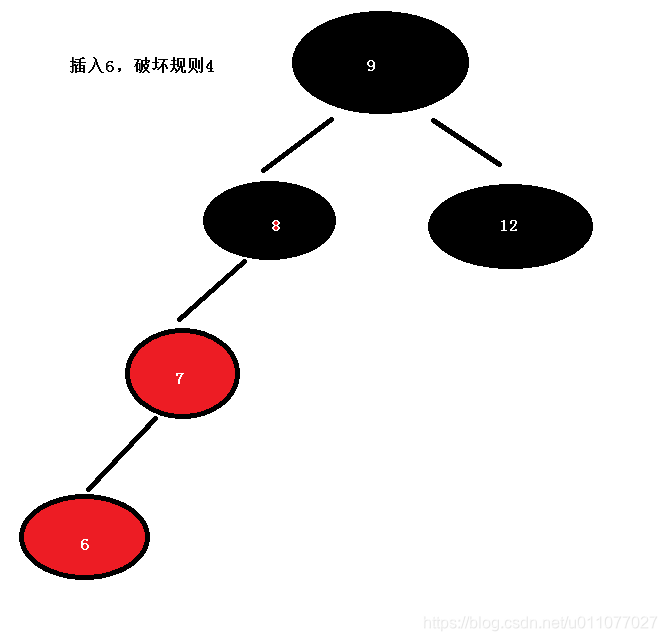
现在新节点 6 是 父节点 7的左节点,而6的叔父节点 缺少,父节点 7 又是祖父节点8的左子节点 ,
这种情形下,我们进行针对6节点的祖父节点8的一次右旋转
右旋转:
顺时针旋转红黑树的两个节点,使得父节点被自己的左孩子取代,而自己成为自己的右孩子。
左旋转则倒过来
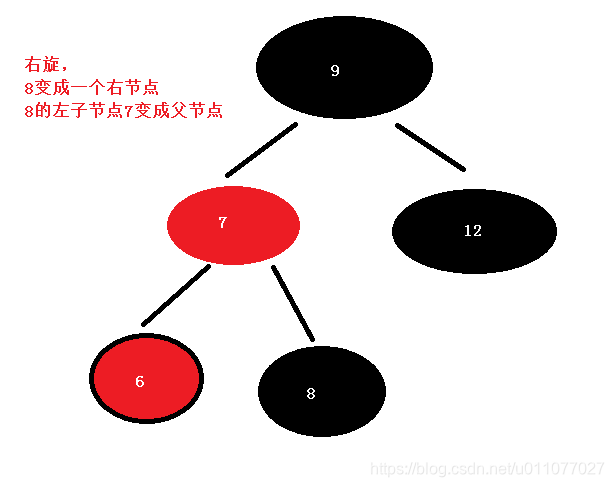
再切换 7 和 8 的颜色
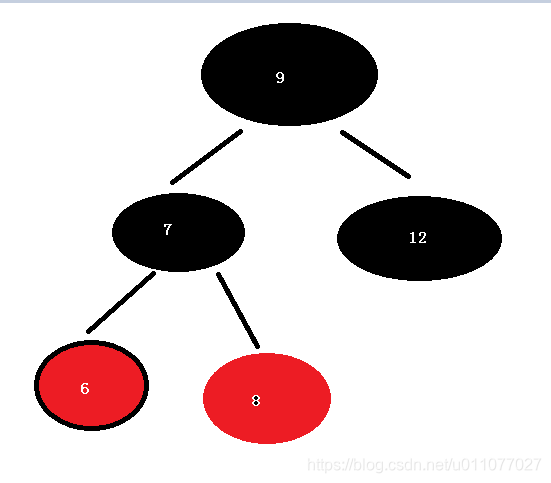
再插入5,5和6都是红色,将 父节点 6 和叔父节点 8 绘为黑色,祖父7设为红色,最终